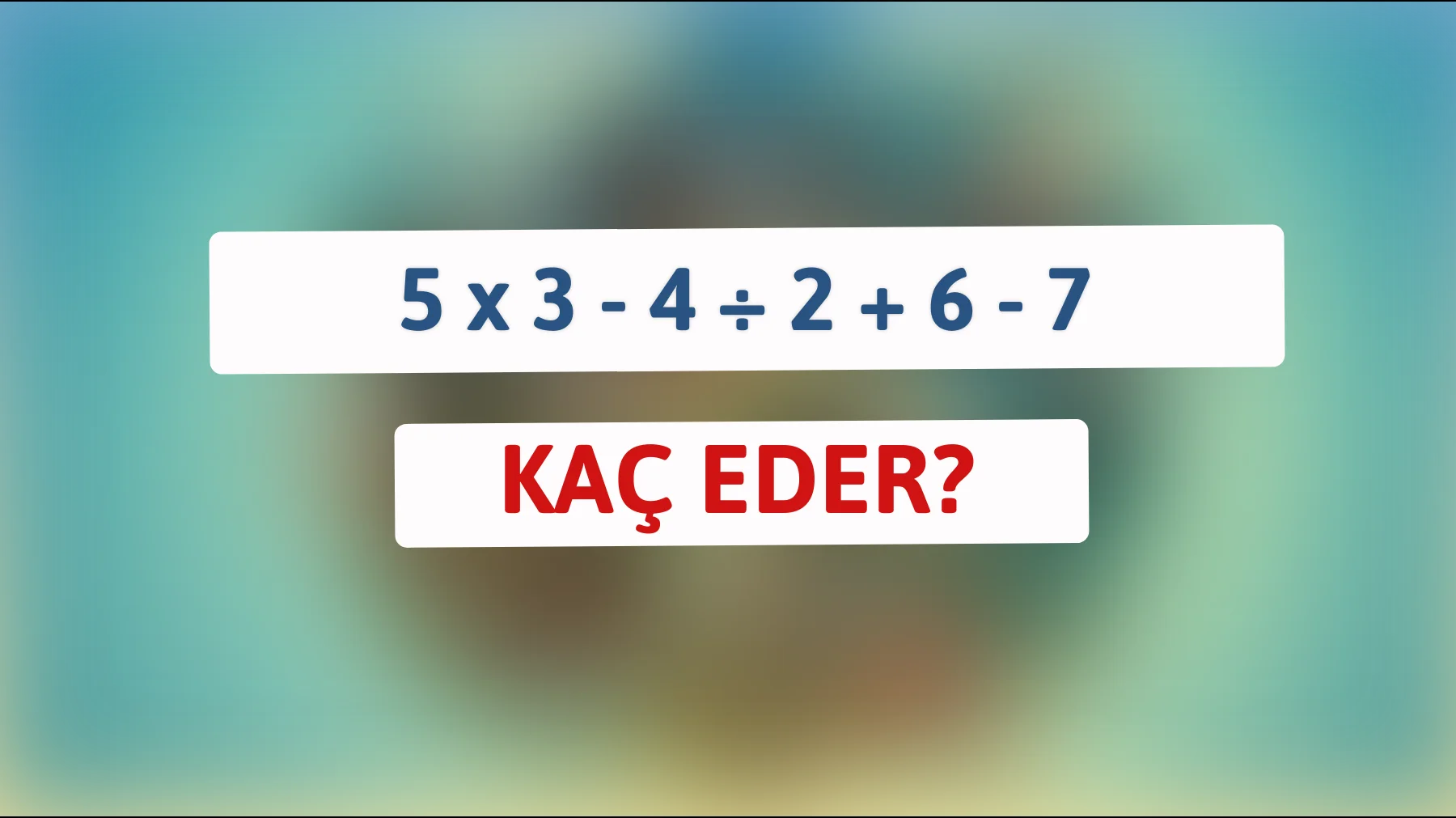Herhangi bir matematik problemi, gizli bir macera gibidir. 5 x 3 – 4 ÷ 2 + 6 – 7 işlemi ise bu macerada size meydan okuyor. Bakalım bu işlemi çözerek cevabın 12’ye nasıl ulaştığını keşfedebilecek misiniz?
Eğer elinizde sadece yağmurlu bir pazar günü ve biraz zaman varsa, bu tür bir zihin egzersizi ile biraz beyin jimnastiği yapabilirsiniz. Buradaki işlem, matematik dünyasında basit bir macera gibi görünse de, arkasında gizemli yollar barındırıyor. İlk önce bu karmaşıklığı aşmak için, işlemdeki temel sıralama kurallarını unutmamalısınız: Öncelik sırasına göre işlem yapma kuralları, yani çarpmalar ve bölmeler önce, toplama ve çıkarmalar sonra yapılmalı.
Belki de, bu tür işlemlerle çok karşılaşmadığınızdan ötürü basit bir hata yapabilir ya da işlemin karmaşası sizi biraz ürkütebilir. Ancak her zaman olduğu gibi, sakin bir zihin ve doğru bir yaklaşım ile çözüme rahatlıkla ulaşabilirsiniz. Matematiğin doğasında yatan bu sırayı takip ederek, ilk bakışta karmaşık görünen problemleri basamak basamak çözmek mümkündür.
Matematik Problemi Çözme Teknikleri: Beyin Egzersizi
Bu tür işlemleri çözmeye başlarken, işler kilidi nasıl açacağınızı bilmek gibidir. **5 x 3** ifadesi üzerinde başlıyoruz çünkü çarpma işlemleri öncelikli. Buradan **15** elde ediyoruz. Ardından, ikinci sıradaki öncelikli işlem olan **4 ÷ 2**’ye bakıyoruz ve buradan da **2** sonucunu alıyoruz. Şimdi, elde ettiğimiz bu sonuçları orijinal denklemdeki yerlerine koymak zamanı.
Elinizde artık şu ifade var: **15 – 2 + 6 – 7**. Bu noktadan itibaren işlem sol baştan yapılır. **15 – 2** işleminde **13** elde ederiz. Bir adım daha atlayıp **13 + 6** yaptığımızda **19** sonucuna ulaşırız. Ve son olarak, **19 – 7** işlemi bizi hedefe yani **12** sayılarına götürür.
Matematiksel Kavrayış: Sayıların Dünyası
Tüm bu işlemi çözdüğünüzde ve sonuca ulaştığınızda, kendinizi bir dedektif gibi hissedebilirsiniz. Ama durun, daha fazlası var: **12**, yalnızca bir sonuç değil, aynı zamanda matematik dünyasında özel bir konuma sahip. 12, “çarpanları bol sayı” olarak bilinir çünkü 1, 2, 3, 4, 6 ve 12 toplamda 6 farklı böleni sayesinde kendine yer bulur. Matematikteki bu tür özellikler, sayıların sadece bireysel semboller olmadığını, aslında evrensel bir dil olduğunun en iyi kanıtıdır.
Belki de bir sonraki matematik buluşmanız tam karşınızda duruyordur, sadece biraz odaklanmanız gerek. Unutmayın ki, her sayı, her işlem tarzı bir fırsat sunar. Gördüğünüz gibi, basit bir işlem karşında dahi bambaşka dünyalara açılan bir kapı bulunmakta. Şimdi sıra sizde; başka bir matematik problemiyle sınırları zorlayarak keşfetmeye devam edin!